
 |
||||

 Contents
Contents
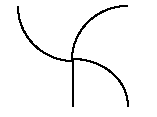
Fig 1 Smooth continuation of lines

Fig 2 Preferred visual grouping of lines

Fig 3 This visual grouping of lines is normally rejected (even though it was the grouping that was used to create Fig 1)
Perhaps this feature derives from our experience of the 'objectness' of things. Thus, we see objects as a whole even when they are partially occluded by other things because we know that they do not break up when they disappear from view, as Figure 4 shows. Objects overlaying others have continuous outlines. The overlaid objects have interrupted outlines but, by the principle of smooth continuation, we can deduce continuity behind the overlaying object. Kellman and Spelke (1983), however, show that 3-4 month old infants only appreciate this if the objects are moving relative to one another.
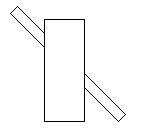
Fig 4 Smooth continuation contributes to our feeling of 'objectness' and allows us to judge that the thin rectangle might be a complete object behind a rectangle in front
Presumably we learn to judge the still-image situation from experience although, as Figure 5 illustrates, our tendency to accept objectness through the principle of smooth continuation can sometimes mislead us.
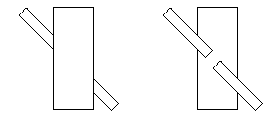
Fig 5 Sometimes objectness overrides smooth continuation and gives us the mistaken impression that lines continue when they do not. Not only is the diagonal rectangle in the left hand side of the figure not continuous, the two diagonal rectangles (as can be seen in the figure to the right) do not even align
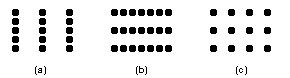
Fig 6 The principle of proximity determines our interpretation of the groups
Obviously proximity and the size of the elements that make up the pattern are related factors here (Zucker and Davis 1988).

Fig 7 The principle of similarity determines our interpretation of the groups in this case and thus we tend to see diagonal lines
Sometimes, similarity can override proximity as the organising principle (Figure 8).
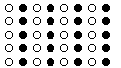
Fig 8 The principle of similarity ensures that we group the dots in vertical columns
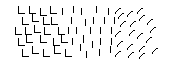
Fig 9 We group together items having similar orientations rather than similar shapes
Orientation, as we shall see later when we look at relationship to frame, also affects our interpretation of a shape.
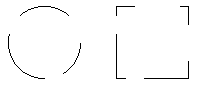
Fig 10 The principle of closure determines that we see these interrupted lines as forming closed figures
Thus it is often possible to suggest a virtual frame around a figure by only drawing its corners. The organisational principle of closure seems to come to the fore when we interpret sketch drawings - which are often incomplete but which we normally have little difficulty in understanding (Figure 11). See also Productive ambiguities in drawing p66.

Fig 11 Closure comes into play in our recognition of sketches

Fig 12 We tend to read this image as a white square on a black one rather than a black square with a hole in it
When there is little difference in the size of the parts, ambiguity can result and we are unable to fix exactly which is the figure and which is the ground. Sometimes this ambiguity can be exploited for art purposes. Figures 13 illustrate this.

Fig 13 Two versions of an image in which the relative sizes of the parts are similar so that it is difficult to distinguish figure from ground (based on a CND poster)
In cases like these we can chose arbitrarily which is the figure and which is the ground. One choice allows us to perceive one meaning, the alternative choice allows us to perceive a different meaning. This effect is the basis of a number of well-known optical illusions such as the faces/vase illusion of Figure 14.

Fig 14 Different information arises depending on whether we take the black or the white to be the ground
Part of the ambiguity of Figure 14 seems to derive from the mixture of convexity and concavity of the black and white parts. Kanizsa and Gerbino (1976) show that shapes that are symmetrical about a vertical axis are usually seen as figures against ground but that this is not always the case if the forms are concave. Carrying out experiments with diagrams similar to those shown in Figure 15, they discovered that over 92% of people tested see the convex shapes as the figures and the concave ones as ground. This is independent of whether the convex shapes are black as in (a) and the concave ones white, or vice versa as in (b).
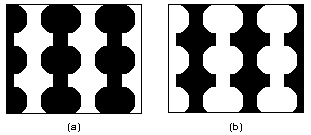
Fig 15 In general it is the convex shapes that are seen as figures against ground
To check whether the matter is influenced by degree of symmetry rather than convexity/concavity, Kanizsa and Gerbino (1976) went on to test subjects using diagrams similar to those in Figure 16 in which the concave shapes are symmetrical about the vertical and horizontal axes but the convex figures are only symmetrical about the horizontal axis. Once again the overwhelming majority of subjects saw the convex shapes as the figures whether they were drawn in black, as in Figure 16 (a) or in white, as in Figure 16 (b).
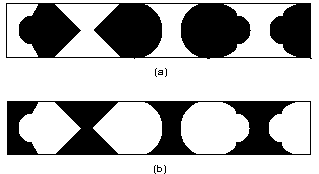
Fig 16 Here again, the convex shapes are seen as figures on a ground of the opposite colour
This seems to confirm an innate preference for convexity in two-dimensional shapes. It is not clear, though, that this preference transfers to a preference for convexity in the third dimension (although this can probably be inferred).
As with the other grouping principles, the figure/ground, relative size principle can sometimes be overridden by a different preference: in this case for certain orientations (as in Figure 17 where, in both images it is the upright one that dominates).
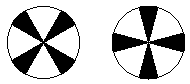
Fig 17 Our perception of what is figure and what is ground changes with the orientation of the figure suggesting that orthogonal relationships are preferred
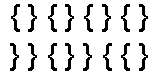
Fig 18 Symmetry is a strong grouping principle. It is very much easier to make sense of the top line of the figure than the bottom one
It is known that we make less eye movements when dealing with symmetrical figures and it is probable that they take less cognitive resources to process.
Like all the principles, symmetry can also be upset by context. Thus the dot in the centre of the square in Figure 19 can appear not to be in the centre when an additional off-centre square is added.

Fig 19 The addition of an off-centre square upsets our perception of the central dot

Fig 20 This familiar image is hard to recognise in this orientation. Turning the image through 90 degrees clockwise allows us to view it in 'correct' orientation
Our sense of 'objectness' often comes into play: knowing that we are looking at a partially occluded object immediately affects our ability to group. This is strikingly illustrated in Figures 21 and 22
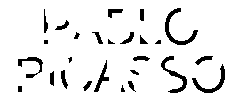
Fig 21 It is difficult to make sense of this image . . .
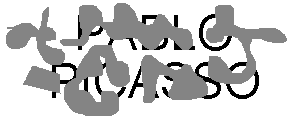
Fig 22 . . . until one realises it is partially occluded text
The context with which we frame a drawing is also significant. The squares and diamonds in Figure 23 are perceived differently according not, as might be supposed, to their relation to some absolute frame of reference, but to their placement within the drawing frame. This has obvious implications for the design of Virtual Environments, where the user's frame of reference - the sense for example of 'right way up' - is all too easily lost.
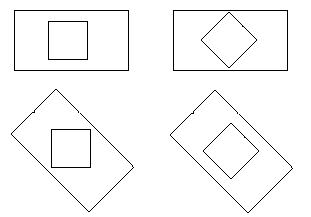
Fig 23 The relationship of the internal figure to the orientation of the frame determines whether we will perceive it as a square or a diamond
Palmer (1992) has shown that context is also significant in allowing us to orientate ambiguously pointing shapes such as equilateral triangles. When seen alone, an equilateral triangle can appear to point in any of three directions (In Fig 24 a the triangle can be seen as pointing to 3 o'clock, 7 o'clock or 11 o'clock). When seen grouped in company with similarly orientated triangles, all seem simultaneously to point in one or other of these directions (Fig 24b). The preferred direction of pointing changes when the triangles are aligned along an axis (Fig 24c). When they are aligned along one of their sides, they seem to point in a direction at right angles to the alignment (Fig 24d).
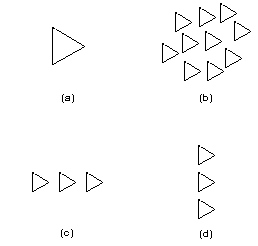
Fig 24 Equilateral triangles have ambiguous orientations that can be directed by appropriate grouping
Note the even more ambiguous effect of arranging similarly orientated triangles around a circle (Fig 25).
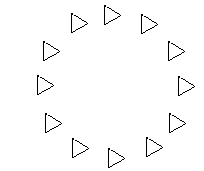
Fig 25 It is hard to perceive these equilateral triangles as having the same orientation

 Contents
Contents
Graphics Multimedia Virtual Environments Visualisation Contents