
 |
||||

 [Top]
[Top]Review of Visualisation Systems
When selecting a visualization algorithm, it is useful to first consider the nature of the underlying field. What are the dimensions of the independent variables? What are the datatypes of the dependent variables, and so on.
Indeed we shall use the nature of the underlying field as our means of classifying the visualization algorithms. We use a subset of the classification derived at the AGOCG Visualization Workshop in 1991 [11].
The letter ![]() represents the entity to be visualized, and a subscript denotes the dimension of the independent variables. Thus
represents the entity to be visualized, and a subscript denotes the dimension of the independent variables. Thus ![]() represents an entity defined over a 3D region. Time is treated specially - so in the above example, if the entity varies over time, we write
represents an entity defined over a 3D region. Time is treated specially - so in the above example, if the entity varies over time, we write ![]() .
.
The type of dependent variable can be scalar (![]() ), vector of dimension k (
), vector of dimension k (![]() ) or tensor (
) or tensor (![]() ), and this is written as a superscript.
), and this is written as a superscript.
So a vector field over 3D is written as: ![]() .
.
There are a variety of methods and a good reference is the book by Lancaster and Salkauskas [44]. Here we give only a brief summary.
Consider first just
The simplest method is nearest neighbour, in which the value of F is taken to be the f-value of the nearest datapoint to x. Notice two features: it is very quick; but F(x) has a discontinuity midway between each datapoint.
Continuity can be improved by linear interpolation, in which F(x) is a linear function (that is, a straight line) between data points. This requires some computation so is slower, but F(x) is now continuous. Note however the slope of F(x) is not continuous, so if we know the underlying entity is smooth, then our recreation of it may be misleading in this sense.
Slope continuity (continuity of the first derivative of F(x)) can be achieved, but at the expense of more computation. A usual method is to estimate the slopes at the data points (for example, as the average of the slopes of the lines to adjacent data points) and then to fit a cubic function in each interval between data points. There are a variety of techniques for doing this piecewise cubic interpolation [12].
Second derivative continuity can be achieved, at even more computational expense, using cubic splines.
There are analogs of these methods in 2D and 3D. Consider first data on a rectilinear grid. The nearest neighbour extends in an obvious manner - it is quick, but discontinuous as in 1D.
Linear interpolation extends to bilinear (2D) or trilinear (3D). Bilinear interpolation proceeds thus: find the grid square of interest; use linear interpolation in x for both extreme values of y; use these two calculated values in a further linear interpolation step in the y-direction. Trilinear is an obvious extension to 3D. These give continuity of function value, at extra computation expense. Hill [21] describes computational aspects of linear, bilinear and trilinear interpolation.
It is important to note that the bilinear interpolant in 2D is deceptively complex to visualize: it is a curved surface with contour lines which are hyperbolic. Similarly, the trilinear interpolant in 3D is likewise complex: surfaces of constant value are hyperbolic in nature. For this reason it can be useful to split the rectangles into triangles, or cuboids into tetrahedra, and fit simpler interpolants in each triangle or tetrahedron. These have straight line contours, or planar surfaces of constant value, respectively.
Piecewise cubic interpolation extends to piecewise bicubic and piecewise tricubic; these provide first derivative continuity, but are relatively rare (especially tricubic) on account of the computation involved.
Suppose now the data does not lie on a rectilinear grid. A variety of techniques have been suggested for scattered data, and a good recent review is by Foley and Nielson [16]. A very simple and reliable method is multiquadric (MQ) interpolation. The MQ interpolant is continuous in all derivatives, and is defined (in 2D) as:
where
with R a constant and d the distance of (x,y) from the ith data point (xi,yi). The coefficients ai are found by solving the N linear equations:
The extension to 3D (and indeed higher dimensions) is straightforward.
Another good method is the quadratic Shepard's method. This has the form:
where Li(x,y) is a quadratic function constructed to be a good approximation to the underlying function near the corresponding data point (xi,yi), and wi(x,y) is a weighting based on the distance of the interpolation point (x,y) from the corresponding data point. Again the extension to 3D is straightforward.
Another approach is to construct, in 2D a triangulation of the data, or in 3D a tetrahedral decomposition. There are well known algorithms for this: the Delaunay triangulation has optimal properties in terms of avoiding long, skinny triangles - traditionally thought to be a good thing. (Note however that views on this are changing - data dependent triangulations that align the triangles with features of the data, rather than across them, can give superior results in practice - see the paper by Dyn et al [14])
The triangulation is useful because local interpolants can be fitted within each triangle. Again these can be linear to give function value continuity, or higher order to give slope continuity.
There are many other techniques for interpolating scattered data, and the reader is referred to [16] for detail. Renka [60] gives an efficient implementation of the quadratic Shepard method.
A large class of applications require the visualization of a scalar field over a 3D region. For example, data from medical scanners, temperature or pressure data from CFD.
There are essentially two approaches:
3.3.3 Interpolation
Interpolation is the process by which the empirical model is created from the data.![]() . We shall be given a set of points
. We shall be given a set of points ![]() . The interpolation problem is to construct a model F(x) which matches the data at the given points.
. The interpolation problem is to construct a model F(x) which matches the data at the given points.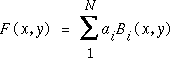
![]()
![]()
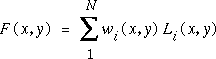
3.3.4 Algorithms for scalar data over 3D
![]()
We now look at these approaches in greater detail:
Of course, these techniques display only a 2D subset of the data. However, the third dimension can be visualized through animation - in the case of slicing, the cross-section can moved in time through the 3D region; in the case of isosurfacing, the isolevel can be moved in time from minimum to maximum.
Note that in the case of an isosurface, it is possible to visualize a second scalar field over the extracted surface, by assigning colour values to the surface corresponding to the second scalar field.
Surface Extraction
Slicing
This is relatively elementary: the slice can be positioned anywhere in the volume, a special case being the orthogonal slice which is perpendicular to one axis. A typical visualization technique on the slice is the image display, in which each pixel is coloured according to the scalar value at the corresponding position on the slice; but other 2D techniques are possible (e.g. contour lines). The 2D algorithms are described in section 3.3.6.Isosurfacing
The extraction of isosurfaces has been studied in detail by researchers over the last few years. An excellent review article has recently appeared [49].
The best known algorithm is marching cubes [47]. This assumes data defined on a set of cubical cells, and constructs a polygonal approximation to the isosurface on a cell-by-cell basis. The extraction uses linear interpolation along edges of the cube cells, and a simple strategy to determine the surface across faces and in the interior. This strategy needs some care however, as topological ambiguities can occur, and as a consequence there can be holes in the resulting surface. Ning and Bloomenthal [49] explain how this can occur, and the remedies which can be taken. Certainly a good algorithm will contain some robust disambiguation strategy.
One such strategy is to decompose each cell into a number of tetrahedra. If this is done carefully - again see Ning and Bloomenthal - then linear interpolation along edges is sufficient to uniquely define a piecewise linear interpolant within each tetrahedron, and hence an unambiguous surface over the entire volume. This is known as marching tetrahedra.
Other strategies are possible, and some are more efficient than marching tetrahedra because they generate fewer triangles.
If the data are not given on a structured mesh, then there are techniques to construct a tetrahedral mesh from the data
Marching tetrahedra can then be used on this mesh.
A common feature of all algorithms is the generation of a set of triangles which approximate the isosurface. These are passed to a geometry renderer for display. For lighting and shading, it is important to calculate surface normals at the triangle vertices, and different strategies are possible:
As mentioned earlier, the colour of the isosurface may be assigned by some transfer function of a second scalar field.
There are a variety of techniques for the display of vector field data. For a good review, see [50] and [22]. We summarise the main techniques here:
It is possible to show a second scalar field by draping a colour shaded contour map over the surface - that is, one scalar variable is represented by height, the other by colour.
There are also some other related modules that can be used in conjunction with the Plot module to produce other 2D representations of data.
IRIS Explorer release 3.0 will also have NAGGraph with more advanced features than Graph.
There are numerous operators in the Image Toolbox which are general image processing operators and more information is given in section 3.4.8.
Xprism can also produce line, mesh, coloured contour and shaded 3D plots. There are also facilities to alter annotation and parameters associated with these plots within Xprism.
Generated with CERN WebMaker
Graphics Multimedia
Virtual Environments Visualisation
Contents
3.3.5 Algorithms for vector field over 3D
This is the type: ![]() . The field is defined by position only, that is, it is time-invariant or steady.
. The field is defined by position only, that is, it is time-invariant or steady.
It should be noted that it is often useful to calculate scalar quantities from the vector field, for example:
There are serious perception problems when this technique is used in 3D. It is more successful when a 2D surface is extracted, and the arrows are shown only for data points on the surface - indeed it is often effective to draw only lines without an arrowhead giving a spiked appearance (hence the term "hedgehogs"). Some success has been obtained in 3D by using 3D glyphs.
In practice, this visualization technique is implemented as follows. An initial particle position is specified: say ![]() , at time
, at time ![]() . Then its progression is governed by the system of Ordinary Differential Equations (ODEs):
. Then its progression is governed by the system of Ordinary Differential Equations (ODEs):![]()
with the initial values:![]()
Because the flow is steady, the velocities vx, vy and vz are dependent only on position, not on time. The solution of these equations is done numerically, and the quality of the ODE solver will determine the accuracy of the resulting path. Euler's method is simple and quick, but generally inaccurate. Better results will be gained by a Runge-Kutta method. There are a family of R-K methods, with differing orders of accuracy. Second order R-K is commonly used.
The solution will also need interpolation to calculate the velocity at the points required by the ODE solver, and the different algorithms described earlier can be used.
The presentation can be as the animated movement of the particle, or the trace of the particle path can be rendered. In this latter case, the path is identical to a stream line as explained below.
For steady flows, particle paths and stream lines are identical, and so the computation process is identical. The user will typically provide a set of starting positions from which the stream lines are generated.
In practice, this can be computed by selecting initial positions on a line in the flow. These are imagined as the start points of particle paths, and the positions of the particles at regular time intervals are recorded - interpolation through the positions at any time gives the corresponding time line.
These scalar quantities are of type ![]() and can be visualized as such.
and can be visualized as such.3.3.6 Scalar field over 2D
There are three approaches:
These approaches are described in more detail:
Alternatively, the line can be extracted in the space of the dependent variable, giving a line (an isoline or contour line) along which the scalar field has constant value. Several isolines can be drawn, within a range of values of the scalar function, so as to give a view of the whole region. A variation is to shade with constant colour between isolines.
Line Extraction
This is elementary: typically values along the slice direction are extracted, and a simple graph is drawn. The 1D interpolation techniques mentioned earlier can be used to fill in between the extracted samples.
There is a vast literature on contouring which has been a popular 2D visualization technique for geographers and other scientists for many years. A good review paper is by Sabin [61].
Methods based on linear interpolation will have slope discontinuities as the isolines move between grid cells. For smoother lines, one needs a method based on bicubic interpolation - see Preusser [51].
For scattered data, one approach is to create a triangulation of the data points. Within any triangle, the intersection of the isoline with the edges can be found. Joining the intersections with straight lines gives the isoline of a linear interpolant within the triangle.
An alternative approach for scattered data is to use an interpolant to estimate the underlying field on a grid, and then use a gridded contouring method. It is often useful to enhance the appearance by shading the regions between isolines - indeed the isolines may be removed altogether. As with volume rendering, one needs a colour transfer function to associate colour values with values of the underlying field.
Surface Drawing
Another traditional graphics technique for 2D data is the carpet plot which shows 2D scalar data as a surface in 3D space - the value being mapped to the height axis. In earlier days this was drawn as a projection of a network of 1D curves parallel to the x and y axes, giving the carpet like effect. Modern implementations will draw this as a smoothly shaded surface. Image Display
This is a very simple technique in which the sample region is mapped to a corresponding region on the device, and the colour of each pixel is determined by the associated value, or interpolated value, at that point. Again a colour transfer function will achieve this.3.3.7 Scalar field over 1D
This we mention largely for completeness: the conventional approach is to draw a graph, relying on one of the interpolation methods described in section 3.3.3 to fill in between data points.3.3.8 AVS
Scalar field over 3D
Note: AVS has separate modules for different datatypes - ucd data is treated by a separate set of modules from AVS field data - field data can be uniform, rectilinear or irregular grids.
Slicing: The orthogonal slicer module takes a slice through a 3D scalar field, perpendicular to one of the axes.
The arbitrary slicer module takes a slice at any orientation. The thresholded slicer module is similar, but any values outside a range are mapped to zero in the output slice.
For ucd data, the slicing module is ucd rslice.
The isosurface module generates an isosurface from a 3D scalar field. The particular algorithm used is not described in the manual. Likewise the way that gradients are calculated is not described.
The ucd iso module does the same for ucd data.
The surface may be coloured by a second scalar field.
The tracer module creates a ray cast image from volume data. There are two interpolation methods: voxel approximation which is similar to nearest neighbour in that the voxels are deemed to have constant colour and opacity, but the value is taken from the upper left corner of the cell; and trilinear interpolation.
The cube module is a general tool, adapted from SunVision, which has four options: texture - which shows texture-mapped exterior surfaces of the volume; maximum - which just projects the maximum voxel along each ray; ray cast and create surfaces - which render surfaces at different density levels by ray casting.
The xray module is a fast volume renderer, giving orthographic views only of the data.
The volume render module - the exact technique being used is not clear from manual - allows the rendering of volume and surface data in combination.
Vector field over 3D
Note: The AVS modules described below apply to static vector fields.
The hedgehog module shows arrows at locations in the 3D volume - for AVS node data. These locations may be generated first by the sampler module, and can be: single point; points on line or circle; points on plane; points in volume; data points themselves.
The arrows can be drawn with or without arrowheads.
Note: A scalar field can be viewed in conjunction with the hedgehog by colouring the arrows according to the value of the scalar field at that point.
The ucd hog module does the same for data defined in the AVS ucd data structure.
The particle advector module releases a grid of particles into the field. As with hedgehog, the initial sample of points can be generated by the sampler module. The particles can be displayed as a tracer of specified length, and batches can be released.
The ODEs can be solved either by Euler's method, or Runge-Kutta (order of R-K method not specified in manual). Interpolation method is not specified.
There is no standard UCD Particle Advector module but a public domain module ucd_particle makes use of the ucd_streamline module to display particles along each streamline segment.
The stream lines module generates stream lines for a vector field. The user can specify the initial sample of points from which the stream lines are drawn.
The ODEs can be solved either by Euler's method, or Runge-Kutta (order of R-K method not specified in manual). Interpolation method is not specified.
The ucd streamline module is similar for ucd data. The ODE method has choice between Euler, 2nd order R-K and 3rd order R-K.
The stream lines module can optionally create a surface connecting the stream lines.
The ucd streamline module can optionally create ribbons of specified width.
Scalar field over 2D
The contour to geom module constructs isolines from a 2D scalar field for a specified threshold value. The particular technique used is not described.
The ucd isolines module creates isolines on the exterior boundary of a UCD structure.
The colorizer module converts data at each point of a scalar field to a colour.
Scalar field over 1D
AVS provides the module AVS/Graph (contained in AVS release 5.02 which is now available) for producing traditional 2D plots from 1D data. The module has been built using some of the Toolmaster-agX libraries and is an example of AVS and UNIRAS integration. The module provides a number of different representations of the data:
The module provides the usual control over parameters and annotation facilities: title, axes, limits, line/curve/marker styles etc.3.3.9 IBM Data Explorer
Scalar field over 3D
Slicing: The Slice module extracts an orthogonal slice through a volume of data, and this can be passed to a 2D visualization technique.Slice extracts an n-1 dimensional slice from an n dimensional dataset. The nth dimension is removed, i.e. a Slice from a 2D dataset produces a 1D line, a Slice through a 3D dataset produces a 2D grid (with no third dimension).
Slab does a similar job to Slice except it maintains the nth dimension of the data and allows the slab thickness to be controlled.
MapToPlane allows users to define non-orthogonal slices by controlling both the position of and normal to the plane
Isosurface: The Isosurface module creates an isosurface from a scalar field. The particular algorithm used is an implementation of marching tetrahedra [41].
The gradient vector (for shading) can be generated internally (again how it does it is not specified), or it can be supplied explicitly. The Gradient module will calculate the gradient of the scalar field, and this can feed into the Isosurface for shading.
The Render module creates a volume rendering of volume data (alternative modules are Display and Image. The data is of the "scalar field" datatype. The algorithm used is specified in [48].
Note that the module can handle a combination of volume data and surfaces.
Vector field over 3D
Static Field
Time Varying Field
The Streamline module produces streamlines for static vector fields. It traces the flow of a particle released from a defined point. The tracing is done by proceeding step-by-step, each step being in the direction of the vector field at the current point; this direction is found by interpolation from the vector data. The user has control over the step length. (This would appear equivalent to Euler's method.)
There is a sophisticated set of controls. The starting points can be given as a list of points, or as a geometric entity - which could be an isosurface for example. The lines themselves can be drawn as lines, ribbons (by connecting to the Ribbon module), or 3D tubes (by connecting to the Tube module).
The Streaklines module produces streaklines for time-varying vector fields. This works as follows. Successive vector fields advancing in time are passed to the module. The streaklines are traced step-by-step as for streamlines, but the direction is calculated now by interpolation in space and time.
Scalar field over 2D
The Isosurface module will create isolines from 2D data. A number of threshold values can be specified. The technique used is not described.
The Band module, together with the Autocolor module, will create a visualization with coloured regions denoting ranges of values.
The Rubber Sheet module can be used to create a surface view.
The Autocolor module converts data at each point of a scalar field to a colour.
Scalar field over 1D
IBM Data Explorer provides a Plot module to provide traditional 2D graphics plot of 1D data. The module provides all the facilities to alter parameters and annotation features associated with the plots. These include: axes labels, title, axes style (linear and logarithmic), tickmarks and colour legends.
3.3.10 IRIS Explorer
Scalar field over 3D
Slicing: The Slice module slices a uniform 3D lattice by taking regular samples on a cutting plane, which may be at any orientation. The output is a 2D lattice of the same datatype and number of channels as the input lattice.
The SliceLat module takes a slice through a 3D lattice and outputs the coloured plane as geometry. The lattice cells are intersected with the slice plane, forming polygons. The polygon vertices are coloured by values interpolated from the lattice values.
Other slicing options are provided by Orthoslice, which generates 2D slices which are oriented with the coordinates of the input 3D lattice, and MultiSlice, which gives geometry output from a number of slice planes.
The IsosurfaceLat module generates an isosurface from a scalar 3D lattice. The algorithm used in earlier releases of IRIS Explorer was based on Marching Cubes, although this has been updated in version 2.2.
The gradient vector (for shading) can be generated internally from the gradient of the scalar field (the Smooth parameter "on"). Alternatively the renderer can generate vertex normals from the geometry of the triangular mesh (the Smooth parameter "off").
The surface may be optionally coloured according to the value of another lattice. The colours used can be controlled by means of a colourmap, which may optionally be passed to the module.
The Contour module generates a set of isosurfaces (i.e. 3D contours) in wireframe. The user has control over the minimum and maximum isolevels, and the number of contours to be calculated. They are generated by calculating contour lines in orthogonal 2D slices of the 3D dataset; the user can control the direction of the slices to be used.
The VolumeToGeom module The VolumeToGeom module uses a volume rendering algorithm to convert a 3D lattice into a geometry. The method used is the so-called hierarchical splatting algorithm of Laur and Hanrahan [45], which fills the space within the volume using screen-oriented planar shapes (or splats). The algorithm uses a small number of large splats in uniform regions of the volume, and fills more detailed areas with a lot of smaller splats. The user has control over the error tolerance associated with the subdivision of the volume, and also over the size and type of the splat, which gives interactive control over rendering time and quality. The geometry produced may be combined with other geometry in the rendering of the final scene (see section 3.4.7), unlike the VolumeRender module (below) which performs direct volume rendering on the input lattice.
The VolumeRender module performs volume rendering on a 3D byte lattice. It offers the choice between two algorithms offering different speed and quality advantages, so the user can trade off between interactivity and quality. The "Transform" algorithm gives interactive rendering speeds for moderately sized datasets, while the "Slicer" algorithm produces high quality images with longer rendering times. In the latter case, the user has interactive control over the number of slices (and so, the quality of the final image).
Vector field over 3D
The Vectors module displays a 3D vector field for a 1D, 2D or 3D lattice having 1,2 or 3 channels (i.e. vectors having 1,2 or 3 components). Vectors are located at the lattice coordinate locations and point in the direction of the data vector field. The vectors may be optionally coloured using a scalar lattice of the same dimensionality and size. They may be displayed as lines, tubes (cylinders) or arrows (cylinders plus cones).
The VectorGen module is a simplified version of the same module - here, each vector is represented as a bi-coloured line segment.
The Streakline module calculates a streakline through a velocity field. It stops when either the new velocity is 0, or when the streak intersects the bounds of the velocity field. The user has control over how each iteration is calculated and displayed. The full solution can be shown or each iteration as it is calculated. The current particle path is shown in red with the old paths in green.
Particle advection is provided by the module ParticleAdvect which was developed as part of the NCSA Pathfinder project (http://redrock.ncsa.uiuc.edu/PATHFINDER/pathrel2/explorer/ParticleAdvect/ParticleAdvect.html)
Scalar field over 2D
The contour module generates contour lines for a 2D lattice (or a 3D lattice - see above). For lattices with several channels, the user can select the channel to be contoured. The lines are coloured according to an internal colourmap; this can be optionally overridden by passing another colourmap to the module.
The DisplaceLat displaces the coordinates of one input lattice by the data values of the other. The two input lattices can be the same. This can be used to create a surface view of a 2D lattice. The user can control the amount of displacement interactively.
The LatToGeom module creates geometry from a 1D or 2D lattice i.e., it produces lines or sheets, depending on the dimensionality of the input lattice. The user can control whether the geometry is produced as points, lines or (in the case of sheets) polygons. The geometry can be optionally coloured via an input colourmap.
The DisplayImg module displays 2D lattices as images. IRIS Explorer also contains a number of image processing modules, which may be used to filter or modify the image before display. See section 3.4.7, below, for more details.
Scalar field over 1D
IRIS Explorer currently has two modules which support traditional 2D representations of 1D scalar data. These are:
There is also a Histogram module which can be used in conjunction with the above.3.3.11 Khoros
All the image operators are written tooperate on width-height planes of the polymorphic model. If the depth, time, or elements dimensions of data object are greater than one, the operation is repeated for each width-height plane.Scalar field over 3D
There is an isosurface operator in the Geometry Toolbox which produces an isosurface constructed of triangles. An orthogonal slicer operator is also available. Mapping operators are provided which can map the scalar values contained in the field into RGB-alpha values. Vector field over 3D
There are currently no operators which directly address the visualization of vector fields, although it is possible to produce scalar fields from the vector fields using the various arithmetic operators found in the Datamanip Toolbox.Scalar field over 2D
A two-dimensional field can be produced from scattered location points using the gridding operator found in the Geometry Toolbox. The orthogonal slicer in the geometry toolbox can be used to slice 1D lines from the 2D fields. Two dimensional fields are generally visualized as images or 3D plots, but this is done through various interactive applications.Scalar field over 1D
Xprism can produce a number of traditional 2D plots from 1D data. The Xprism application in the Envision Toolbox provides fifteen different 2D plot types and these include:
The Xprism application also provides full control over fonts, colours, axes, marker types, line types, titles etc.3.3.12 PV-WAVE
Scalar field over 3D
Isosurface: The SHADEVOLUME procedure calculates an isosurface from data in cubical cell arrangement. The algorithm used is that described in [40]. It is said to be variation on marching cubes.
The gradient calculation for shading is not described in the manual.
The VOLREND function in the Advanced Rendering Library creates a volume rendering from data in cubical cell arrangement.
Vector field over 3D
There is only an "arrow" capability for this visualization datatype.
The VECTORFIELD3 function in the Advanced Rendering Library plots vector glyphs at a set of points specified by user. Form of interpolation not specified in the manual.
Scalar field over 2D
The CONTOUR procedure draws a contour plot from a uniform 2D grid, with very sophisticated control over the annotation and presentation. There are two methods: one draws all lines per cell then moves on to next cell; the other traces a line through all cells, then moves to next line. No further algorithmic details are given.
The IMAGE_CONT procedure overlays a contour plot onto an image display. Bilinear interpolation is used in image display.
The SHOW3 procedure overlays image, surface view and contours.
The SURFACE procedure draws a surface view, with sophisticated control over the annotation and presentation.
See contouring above.
Scalar field over 1D
PV-WAVE has a number of specific view windows for producing 2D plots from 1D data:
Each view window provides control over numerous annotation and parameters associated with each view type.
Review of Visualisation Systems

 [Top]
[Top]