Editorial

Abstract

Introduction

The Issues
  Numbers
  Areas
  Symbolism

Dynamic mapping tools

cdv

Alternatives to choropleth maps

Conclusions

Future directions

Acknowledgements

References

Case Studies Index

2.2 Issues concerning the areas

Whatever the numbers used, it should be obvious that the resultant map depends just as much on the pattern of the zones employed in their collection, their shape and areas, as it does upon the phenomenon under investigation. This is one manifestation of the so-called modifiable areal unit problem (MAUP) and it is particularly significant in the analysis of census data because the enumeration areas are almost always relatively arbitrary (see Unwin, 1981,116-119). The MAUP means that virtually any numbers collected over such areas, including the ratios that are displayed on choropleth maps, will depend greatly on the precise boundary definitions used. In the USA most of the state counties are roughly the same spatial area, and this removes some of the worst effects of the problem when we visualise data for aggregations across them. However, the large spatial extent of each state means that there are problems relating to a map projection component in any display of these data as familiar projections do not display equal areas with equivalently sized zones.

In the UK census enumeration districts, which attempt (very unsuccessfully!) to keep a roughly constant population in each unit, vary considerably in areal extent and this can have a very marked effect on the appearance of our maps. Figure 6 is a simple choropleth map of the electoral wards of Leicestershire at the 1981 census shaded such that the shade of grey used in each zone is inversely proportional to its spatial area. It can be seen that there is a pronounced spatial variation in these values, with the zones, or resolution elements (resels?) significantly smaller in the more densely populated areas such as the cities of Leicester and Loughborough. In fact, although it contains absolutely no census population count data at all, this map is very similar to Figure 1, our population density map! Any map of census data using zones of equal population will always have a bias towards the representation of the larger spatial units in the less densely populated rural areas rather than the possibly more interesting intricate detail within the cities. Quite apart from any other statistical considerations, all visualisation of area value data needs to be informed by knowledge about how the zones were defined.

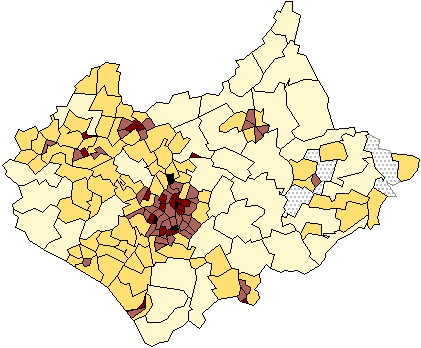
Figure 6: A choropleth map of the electoral wards of Leicestershire at the 1991 census shaded such that the shade of grey used on each zone is inversely proportional to its spatial area.

This area dependence is a fact-of-life in almost all geographical visualisation. To escape it, three radical options have been suggested:

1. The first is to display the census data on what is called a cartogram base. As symbol size is frequently used to signify relative attribute importance it seems contradictory to use a map base upon which symbol size equates with geographic area. This is a largely arbitrary attribute appropriate only if focusing on rural processes, using zone shape to identify the geographic location or assessing distances. In population cartograms the zone areas are themselves expanded or contracted according to the total number of people (the denominator in any population ratio). At the cost of creating what can be a very unfamiliar and seemingly distorted 'geography', this magnifies small areas with large populations at the expense of areas that have very few people. Typically densely populated inner city areas are magnified at the expense of more sparsely inhabited rural ones. It can be argued that the resulting cartography is not only better able to show greatly varying spatial detail, it is also in some sense more socially equitable. In recent years, cartograms have been used to great effect by Dan Dorling to visualise many aspects of the social and census geographies of Britain (for examples, see Dorling, 1995) and code (BBC BASIC, and C) published as part of a very full technical monograph (Dorling, 1996). Figure 7 shows an area cartogram based on the population values for the census zones of Leicestershire created using Dorling's 'circle growing' algorithm.

   

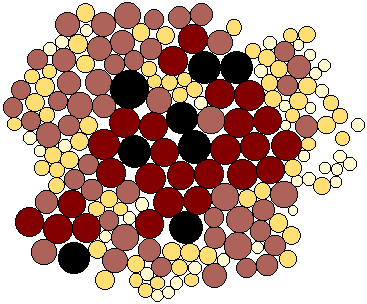
   Figure 7: A non-continuous population cartogram based on the population values for the census zones of Leicestershire created using Dorling's 'circle growing' algorithm. Both the circle areas and shades are proportionate to the zone populations.

   

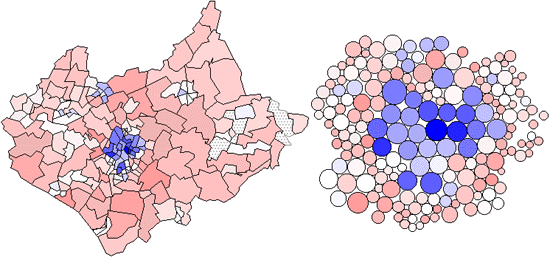
   Colour Figure 4b uses the cartogram base to show the distribution of Figure 4, highlighting the relatively small numbers of people in the identified commuter belt which is over-represented by the land area map due to the large areas which the commuters occupy.

2. The second approach is to transform the census data onto a regular, high spatial resolution grid such as that provided by the Ordnance Survey National Grid, as suggested by Martin (1989). The details are beyond the scope of this case study, but involve interpolation of the census totals from the irregular units onto which they are aggregated by the then Office of Population, Census and Surveys onto a very fine grid mesh of 200m side pixels. These data are readily available for research use by academics in higher education in UK from the MIDAS service at Manchester University. They enable displays of the spatially continuous areal density of population (people per square km) to be created. Figure 8 shows such a surface view of the population of Leicestershire created using these estimates. The view is from the north west, so that we see the towns of Shepshed and Loughborough as `hills' of relatively high population density `in front' of the large `mountain' that is the county town of Leicester.

   

   Figure 8: A surface view of the population of Leicestershire created using the Martin 200m population estimates. The view is from the north west. (Visualisation by courtesy of Kath Stynes, Ravenscroft College)

3. A third approach is to use external information to isolate only those areas within the wards that have residential housing and then calculate the areal densities using these areas rather than the total zone areas as denominator. This is called dasymmetric mapping and it was originally proposed by Wright (1933). In his original study Wright used inspection of a topographic map as a basis for determining the residential areas, but in a recent study Langford and Unwin (1994) used satellite remote sensing to achieve the same result.